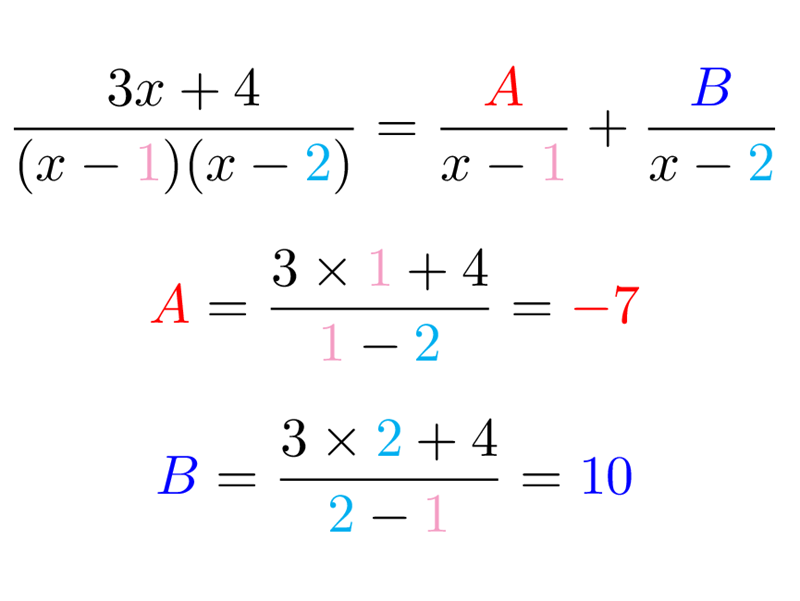部分分数分解とは
部分分数分解とは、分母が積の形の分数式を分解して、分数式の和の形で表すことです。
例えばこんな感じですね。
\[\frac{1}{(x+1)(x+2)}=\frac{1}{x+1}-\frac{1}{x+2}\]
部分分数分解の使いどころ
部分分数分解は、分数関数のグラフの形を考えたり、積分をしたり、分数関数で与えられた数列の和を求めたりするときによく使われます。
グラフを考えるときには大抵その後に最大値を求めたり、微分したりする作業を行いますよね。
つまり、部分分数分解は計算問題の一部分として必要になることが多いといえます。となると、計算ミスはなんとしてでも避けたいところ。
ヘヴィサイドのカバーアップ法を使うと計算量を減らせるので、解く速度を上げ、しかも計算ミスを減らすことができますよ！
普通のやり方
まずは普通に解く方法をおさらいしておきます。
- 分母を因数分解する
- 分解後の分子を文字でおいて、通分する
- 係数を比較して連立方程式を解く
例として以下の分数式を分解します。
\[\frac{4x-2}{(x^2-1)(x-2)}\tag{1}\]
分母を因数分解する
\[\frac{4x-2}{(x^2-1)(x-2)}=\frac{4x-2}{(x+1)(x-1)(x-2)}\tag{2}\]
分解後の分子を文字でおいて、通分する
ここからが割と大変です。
\[\begin{align*}&\frac{4x-2}{(x+1)(x-1)(x-2)} \\ &=\frac{A}{x+1}+\frac{B}{x-1}+\frac{C}{x-2} \\ &= \frac{A(x^2-3x+2)+B(x^2-x-2)+C(x^2-1)}{(x+1)(x-1)(x-2)} \\ &= \frac{(A+B+C)x^2+(-3A-B)x+(2A-2B-C)}{(x+1)(x-1)(x-2)}\end{align*}\tag{3}\]
係数を比較して連立方程式を解く
やっと通分が終わったと思えば、3元連立方程式が待っています。今回の場合は、こうなりますね。
\[\left\{\begin{align*}A+B+C &=0 \\ -3A-B&=4 \\ 2A-2B-C&=-2\end{align*}\right.\tag{4}\]
これをいろいろやって（過程略）、$A,B,C$の値を求めます。
\[\left\{\begin{align*}A &= -1 \\ B&=-1 \\ C &= 2\end{align*}\right.\tag{5}\]
ようやく部分分数分解ができました。
\[\frac{4x-2}{(x+1)(x-1)(x-2)}=-\frac{1}{x+1}-\frac{1}{x-1}+\frac{2}{x-2}\tag{6}\]
速いやり方
次に、速いやり方（ヘヴィサイドのカバーアップ法）です。
分解後の分子を文字でおくまでは同じです。
\[\frac{4x-2}{(x+1)(x-1)(x-2)}=\frac{A}{x+1}+\frac{B}{x-1}+\frac{C}{x-2} \tag{7}\]
ここからいきなり$A,B,C$の値を求められてしまうんです。例えば$A$の値を求めるには、$A$の分母をはらうために両辺を$(x+1)$倍し、
\[\frac{4x-2}{(x-1)(x-2)}=A+\frac{x+1}{x-1}B+\frac{x+1}{x-2}C \tag{8}\]
両辺に$x=-1$を代入します。そうすると、$B$と$C$の項が0になって消えてしまうんですね。
\[A=\frac{-6}{(-2)(-3)}=-1 \tag{9}\]
同じように、$B$と$C$も求めていきます。連立方程式を解かなくていいので、かなり楽です。
$B$を求めるには、両辺を$(x-1)$倍してから$x=1$を代入すると、$A,C$が消えてくれますね。
\[\begin{align*}\frac{4x-2}{(x+1)(x-2)}&=\frac{x-1}{x+1}A+B+\frac{x-1}{x-2}C \\ B&=\frac{2}{(2)(-1)}=-1\end{align*}\tag{10}\]
もう分かってきましたね。$C$を求めるには、$(x-2)$をはらって$x=2$を代入すればよさそうですね。1行目は暗算でいってみましょう。
\[C=\frac{4\times2-2}{(2+1)(2-1)}=2 \tag{11}\]
たったこれだけで分解ができてしまいました！
\[\frac{4x-2}{(x+1)(x-1)(x-2)}=-\frac{1}{x+1}-\frac{1}{x-1}+\frac{2}{x-2}\tag{12}\]
まとめ
やり方を最後にまとめておきます。
- 分母を因数分解する
- 分解後の分子を文字でおく
- 求めたい文字の分母をはらって、それを0にする値を代入する
これであなたも通分&連立方程式の地獄から晴れて自由の身となりました！
それでは、楽しい部分分数分解ライフを！
