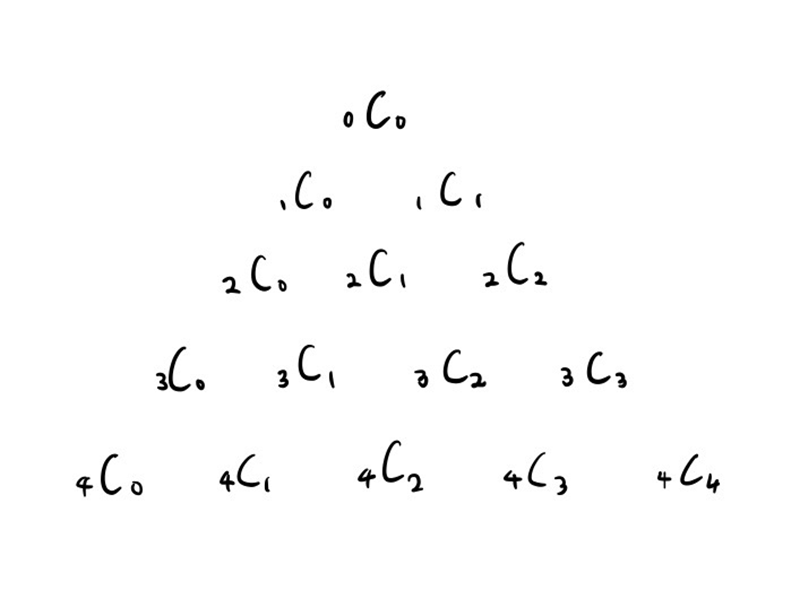導入
パスカルの三角形とは、この図のように規則的に数字を並べたものです。
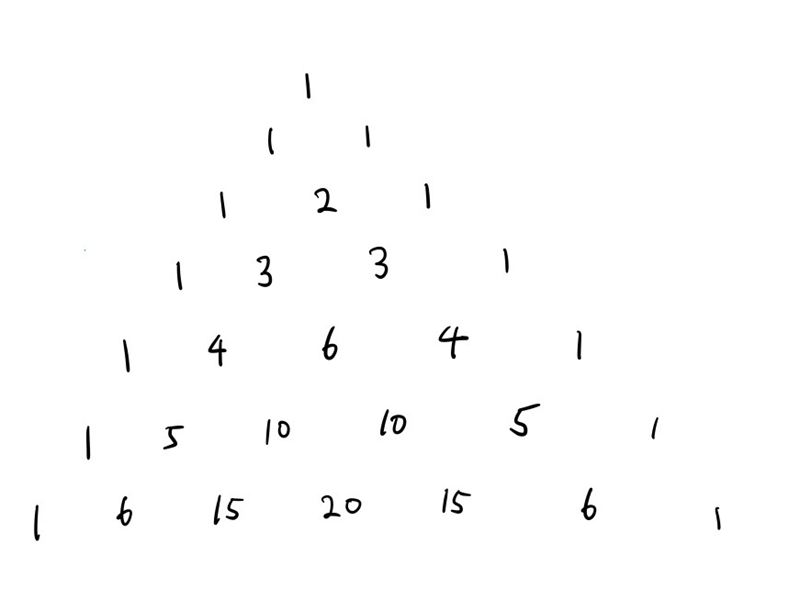
パスカルの三角形には、次のような性質があります。
- 一番上(0段目)は1
- $n+1$段目の数は、右上と左上にある$n$段目の数を足したもの
- $n$段目の右(左)から0始まりで$k$番目の数は${}_{n}\mathrm{C}_k$
これらの性質を使うと、二項係数のさまざまな公式が感覚的に理解できます。
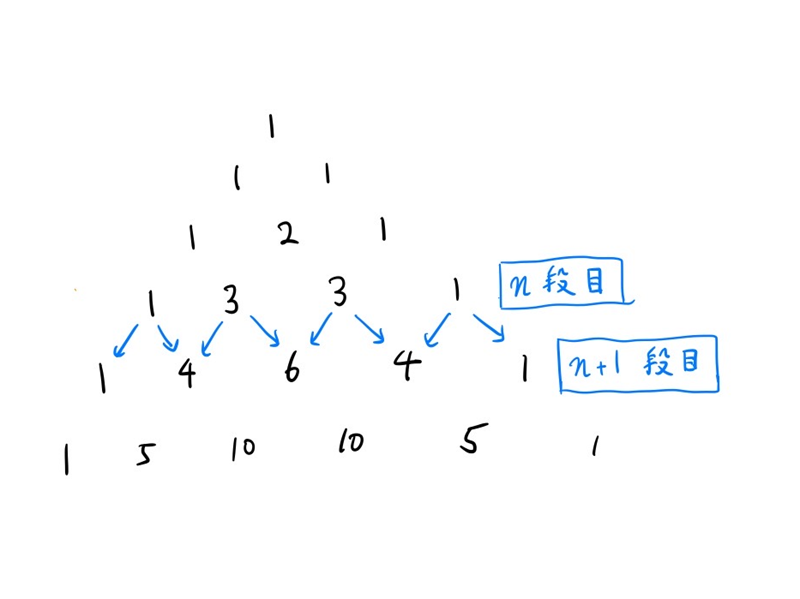
例えば、二項係数の総和が$2^n$になるのはよく知られています:
これは二項定理などでも証明できますが、図において
- $n=0$のとき、成立
- $n$段目の数はそれぞれ$n+1$段目の2つの数に矢印を伸ばしている(ので合計は2倍になる)
ということからも証明できます。
では、逆に$k$を固定して$n$を動かすことにすると、どうなるでしょう?
ここでは、このような、ちょっと踏み込んだ二項係数の和を紹介していけたらと思います。
$n$を動かしたときの和
$k$を固定して$n$でシグマを回したときは、このようになります。
証明
この図を見れば一目瞭然ですね。
斜めの和
${}_{n} \mathrm{C}_0$から始まり、右斜め上の項を足していくこの図のような部分です。
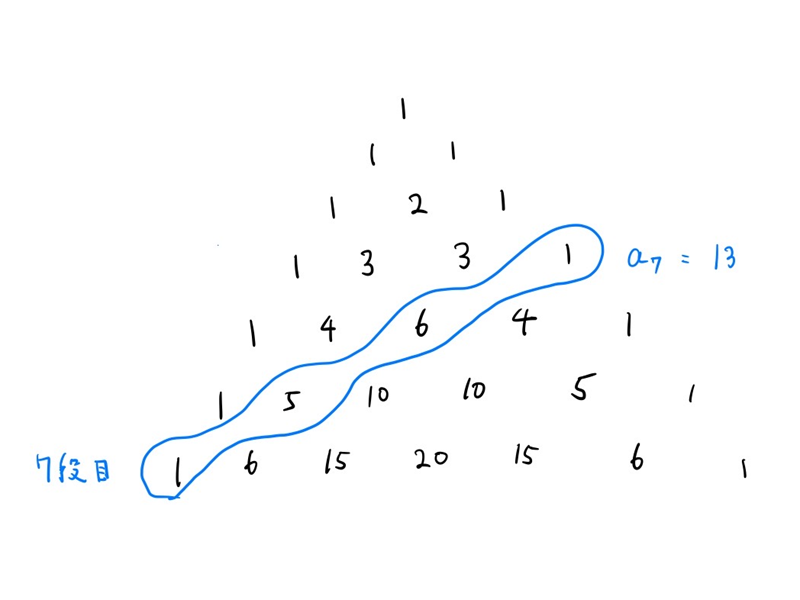
数式で表すとこのようになります。
これはどのように表されるでしょうか?
驚くべきことに、これは$n+1$番目のフィボナッチ数と一致します!
ここで$\phi = \dfrac{1+\sqrt{5}}{2}$は黄金比、$\varphi=\dfrac{1-\sqrt{5}}{2}$は共役黄金比です。
証明
これもパスカルの三角形を使うと導出できます。
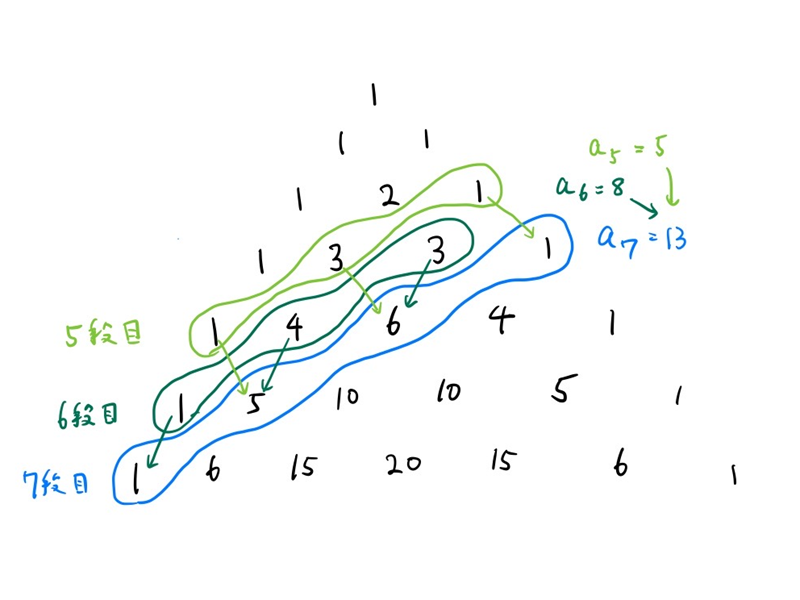
斜めの和の部分をいくつか囲みました。
これをよく見ると、フィボナッチ数列と同じような漸化式が出てくるのが分かります。
- $a_0=1, a_1=1$
- $a_{n+2}=a_{n+1}+a_{n}$
二項係数の積の和
二項係数の積に関して、次の公式(ヴァンデルモンドの畳み込み)があります。
これもパスカルの三角形で証明できるんです。
証明
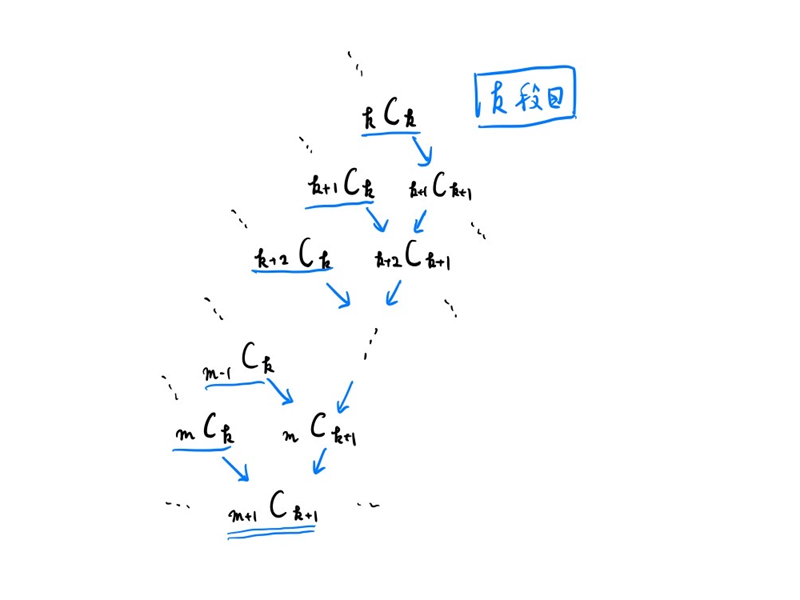
まずパスカルの三角形で${}_{n+m}\mathrm{C}_{r}$を考え、それの$m$段上にある${}_{n}\mathrm{C}_{r-k} (k=0,1,\cdots, m)$を考えます。これらが${}_{n+m}\mathrm{C}_{r}$の中に何回足されたかをカウントしてみます。

ここで図のように、逆向きのパスカルの三角形型を考えると、その回数は${}_{m} \mathrm{C}_{k}$回だと分かり、題意は示された!
終わりに
今回紹介した式をまとめておきます。
数式を用いた証明方法は探すとたくさん出てきますが、今回のように図で理解できる方法はとりわけ理解しやすいですよね。
ほかにも見つかれば追記予定です!