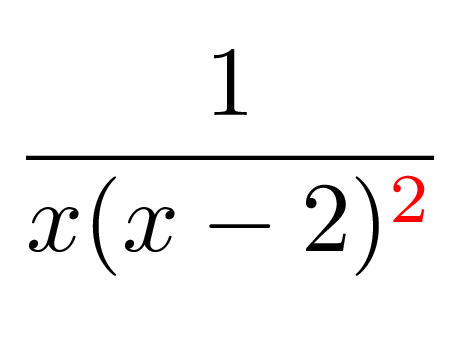分母が2の部分分数分解の方法

分母が2乗、3乗を含む場合の部分分数分解の方法について紹介します！

分母に2乗を含む場合の文字の置き方

次の例で考えてみましょう。

\[\frac{1}{x(x-2)^2}\]

分母に2乗を含む場合は、展開後の分子を定数にするには、分母は

\[x, (x-2), (x-2)^2\]

の3つが必要となります。ここで、$(x-2)$が必要となる点に注意してください。

したがって、部分分数分解後の形は以下のようになります。

\[\frac{1}{x(x-2)^2} = \frac{A}{x} + \frac{B}{x-2}+\frac{C}{(x-2)^2}\]

あとはこの$A, B, C$を求めていきましょう。前回の方法を使えば、$A$と$C$はすぐに求まります：

\[A=\frac{1}{(0-2)^2} = \frac{1}{4}\]

\[C=\frac{1}{2}\]

問題はどうやって$B$を求めるかですね。もちろん、ここまで来ればすべて通分して恒等式を解いても、適当に$x$に値を入れて解いてしまっても大丈夫です：

\[\frac{1}{x(x-2)^2} = \frac{1}{4x} + \frac{B}{x-2}+\frac{1}{2(x-2)^2}\]

ですが、ここではさらに洗練された方法を紹介します！この方法はどれだけ元の関数が複雑になっても計算が煩雑になりにくいです。

それは微分を使う方法です。まず、両辺を$(x-2)^2$倍します:

\[\frac{1}{x} = \frac{(x-2)^2}{x}A+(x-2)B+C\]

ここで両辺を微分します。

\[-\frac{1}{x^2} = \left\{\frac{(x-2)^2}{x}\right\}'A + B\]

最後に、$x=2$を代入します。$A$の項を計算しなくてよいのは、このときに0になるからです。

これで$B$も無事に求めることができました。

\[B=-\frac{1}{4}\]

したがって、最終的な部分分数分解は以下のようになります。

\[\frac{1}{x(x-2)^2} = \frac{1}{4x} - \frac{1}{4(x-2)}+\frac{1}{2(x-2)^2}\]

右辺の$B$の項以外は代入時に0になります。なぜなら、$C$のように、より次数が低い項はすべて微分の過程で0となって消え、$A$のように、$B$より次数が高い項は代入すると0になる因数が残っているからです。

実際に、$(x-\alpha)^2 f(x)$という関数を微分すると

\[2(x-\alpha)f(x) + (x-\alpha)^2f'(x) = (x-\alpha)(2f(x)+(x-\alpha)f'(x))\]

となり、因数$(x - \alpha)$残っていることが分かります。これは一般化しても成り立つので、下の一般式の右辺の微分・代入終了後には求めたい項の定数だけが残っています。

一般に、$(x-\alpha)^n$が分母に含まれる場合、分解後の分母には

\[(x-\alpha), (x - \alpha)^2, \cdots, (x-\alpha)^n\]

の$n$個を含む必要があります。そして、その中の$(x-\alpha)^k$の分子を求めるには、式全体に$(x-\alpha)^n$を掛け、両辺を$(n-k)$回微分した後に$x=\alpha$を代入します。

以上を式で表すと次のようになります：

\[\prod_{i} \frac{1}{(x-\alpha_i)^{n_i}} = \sum_{i} \sum_{j=1}^{n_i}\frac{A_{ij}}{(x-\alpha_i)^j}\]

のとき、

\[A_{ik} = \left. \frac{d^{n_i-k}}{dx^{n_i-k}} (x-\alpha_i)^k \prod_{i'} \frac{1}{(x-\alpha_{i'})^{n_{i'}}} \right|_{x=\alpha_i}\]